Overview:
1. Introduction2. Intuition for Sigmoid function (Hypothesis)
3. Cost function (Maximum Likelihood)
4. Optimization model: Newtons model
5. Derivation for Gradient and Hessian
Lets Begin:
This section is going to be a bit of mathematics. While the Logistic regression can be built just by using the formula, nevertheless it is worthwhile to look how the formula came into being. In this section "Logistic Regression Part-I" we will complete all the math required to understand the logistic regression and in the next we will learn few concepts and implement logistic regression to solve real world problems.Introduction:
Logistic Regression as the name says "Regression" is not actually a regression technique but a classification technique. Classification is a technique in which you find the probability of an occurrence. For example, suppose you have a set of emails labeled as spam and not spam and you build a classifier using these emails as your training sample. With the influx of a new email your classifier will assign a probability value for the email being spam and not a spam.
Logistic regression is not confined to single class classification. It can be stretched to multi-class classification too. For the sake of simplicity lets just consider a single class classifier.
The data-set to the right comprises of "m" training examples (each row) and "n" features (each column). All the rows are labeled as either 1 or 0. For the time being consider it a spam/not-spam training data-set with each example labeled as spam (1) and non-spam (0).
Intuition for Sigmoid function (Hypothesis):
If we recall the blog post on linear regression, for details look here. We know that our hypothesis (h) is defined as:
hθ(x) = θ0 + θ1x1 + θ2x2 + ......... + θnxn
If you look at the hypothesis, you would see that for any random value θ or x the hypothesis may get any value ranging between -∞ to + ∞. But a probability model can only have values between 0 and 1. So what do we do? In-order to convert the hypothesis into a probabilistic model we use the sigmoid function
Sigmoid Function is a S-shaped curve which is also the special case of a logistic function and hence the name logistic regression is derived.
 |
| Sigmoid Function |
The above graph is taken from Wikipedia, I would encourage you to go and read more on Sigmoid function on Wikipedia or elsewhere to have a more detailed understanding.
Applying sigmoid function to our hypothesis, we transform our hypothesis into the below form.
where θT x = θ0 + θ1x1 + θ2x2 + ......... + θnxn
"Voila, we have derived our hypothesis now. What we need now is the cost function and an optimization method to find our optimal parameters. We can always use gradient descent to converge the curve and find the parameters, but we have seen that already here. Going further we shall see a much better approach known as the newton's method to find the optimal parameters"
Cost function (Maximum Likelihood):
Before going into the derivation let us have a quick look on how the cost function of the Logistic Regression model looks.
Now, this is a heck of an equation, by just looking at it one would be confused. The whole formula is nothing but a representation of "Maximum likelihood" for logistic regression.
What is a maximum likelihood estimation?
"The notion on maximum likelihood is that the hypothesis you derive is likely if it makes what you see likely. It is the one that maximizes the probability of the data given the hypothesis."
hML: stands for the maximum likelihood. The above equation says to select a h (hypothesis) among all the H (hypothesis) that maximizes the probability of the actual data or (y).
Since all the data point (y) are independent of each other, the total probability would just be the product of all the independent probabilities given as below.
We know that our hypothesis in discreet, which is, either 1 or 0, we model our yi as Bernoulli's random variable. Therefore using Beroulli's principle on the probabilistic model we get the following equation.
Now we substitute the probability model in our maximum likelihood equation.
Probability of products is computationally difficult, therefore we perform the logarithmic of the whole equation . The advantage of using the logarithm is that the product converts into summation which is easier to deal with and also, log in an increasing function. For example, if you plot a log function of x, increasing x would also increase log(x). Though the values may change as a larger increase in x would result in small increase in log(x) but the maximum doesn't change or the sequence doesn't change. In probabilistic model we are not interested in the values but the candidate that generates highest probability. This candidate would be same for x and log(x).
We use the log properties of multiplication and exponent and compute the above equation.
The above equation shows the formula that maximizes the likelihood (going up hill all the way to the top in the curve). However, finding the local minima is easy in our case cause we have seen optimization techniques like gradient descent that converges to the minimum point. Therefore we convert the whole equation into local minima by prefixing the equation with a -ve sign.
The equation we obtain above is our cost function for Logistic regression. We now just average the whole to get to the minimum value and get out final cost function as:
"Now that we have derived out cost function, let us go ahead and derive the gradient. Surprisingly, you will find that the gradient for both linear regression and logistic regression are the same."
Optimization model- Newtons model:
The Newton method is an advanced optimization method. If you recall the Gradient Descent approach, you will find that the parabolic curve converges or (the minimum cost function) is found after performing the algorithm for many iteration. The iteration can, in some case, be 1000's or even cross 10000's which is time consuming and costly. Reason for such delay is because in Gradient Descent approach the slope of convergence in too small. However, in Newton's method the minimum f(θ) (cost function for logistic regression) can be reached in few iteration.
Intuition:
 The Newton's method takes the tangent from any point in the curve and set the value for the new theta when the tangent meets the x axis (theta axis). This process continues until the minimum f(θ) is reached.
The Newton's method takes the tangent from any point in the curve and set the value for the new theta when the tangent meets the x axis (theta axis). This process continues until the minimum f(θ) is reached.
From the Graph at the right we see that at θ3 the f(θ) is minimum. Looking at the plot it can also be understood that the curve converged in just three iteration (θ1,θ2,θ3,) which is very less.
Now lets go ahead and write the complete formula of convergence for using Newton's method.


Note:
J'(θ) is the Cost function for Logistic Regression
J''(θ) is the Hessian.
Derivation of Gradient and Hessian:
Taking the derivative of the cost function in terms of theta would give us our Gradient.
Gradient:
So now that we have derived the formula for gradient, let's use it and derive the Hessian for Newton's method.








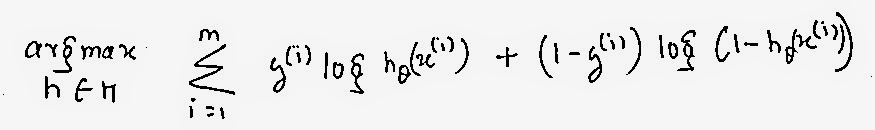


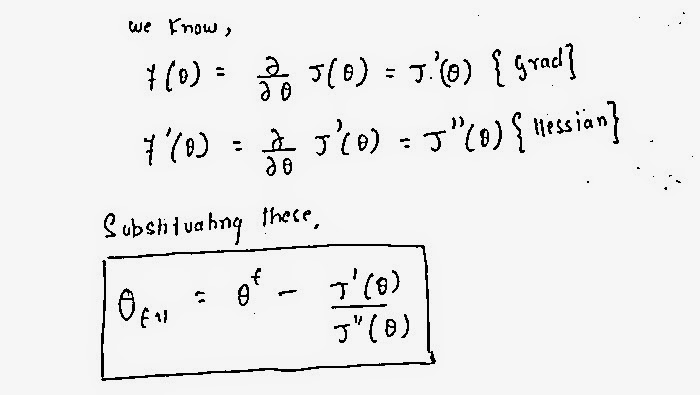















No comments:
Post a Comment